---

Diagrams and Notations

Various diagrams and notations are commonly used by the Sudoku community. As such, these diagrams and notations can be found sprinkled all over Sudopedia. A good part of these are developed so that communication becomes possible in text-based forums, and also for compactness reasons. This article is intended to guide the reader to some of these communications tools.

Although this article refers to several solving techniques, this article merely use them to illustrate diagrams and notations that are used. Since the aim of this article is not to describe these techniques, readers are advised to refer to the various other Sudopedia pages that describe them in more detail.

Contents 1 Givens 2 Pencilmarks 3 Cell Reference 4 Eliminations 5 Single-digit Concept Diagrams 6 Multiple-digit Concept Diagrams 7 Chains and Loops 8 See Also

Givens

In a Sudoku, you are presented with a starting grid with some digits already given in some cells. These digits are usually referred to as givens. Your task is to fill up the remainder of this grid, as described in the introduction. An example grid is shown below. (This grid is rated easy and can be solved using singles alone.)

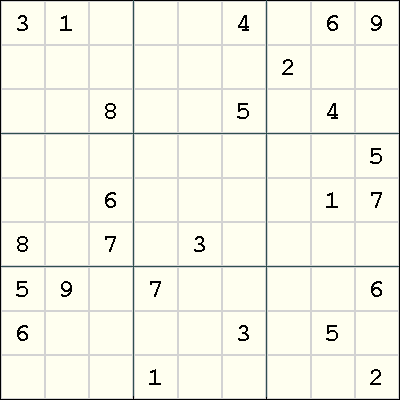
However, in the Sudoku Forums, it is often inconvenient (or sometimes impossible) to upload graphics (e.g. GIFs, JPGs, PNGs). So an alternative text-based format for the same grid is as follows.

.-----.-----.-----.
|3 1 .|. . 4|. 6 9|
|. . .|. . .|2 . .|
|. . 8|. . 5|. 4 .|
:----- ----- -----:
|. . .|. . .|. . 5|
|. . 6|. . .|. 1 7|
|8 . 7|. 3 .|. . .|
:----- ----- -----:
|5 9 .|7 . .|. . 6|
|6 . .|. . 3|. 5 .|
|. . .|1 . .|. . 2|
'-----'-----'-----'

The above format allows easy visualization of the grid, but it takes up a fair amount of screen estate. Sometimes, people want to describe many starting grids in one go, say, as examples that can be solved using a certain solving technique. For such usage, the Sudoku grid is often presented as an 81-digit string. In this format, the digit 0 is used to denote an empty cell and all the values of the cells are concatenated into one long string. So the 81-digit string of the example grid is shown below.

310004069000000200008005040000000005006000017807030000590700006600003050000100002

Most good Sudoku Programs are able to accept such 81-digit strings as input, usually through their paste function. These programs usually also allow users to export the grid in any of the above text-based formats via their copy function.

Pencilmarks

Unless a given Sudoku grid can be solved using singles alone, most Sudoku players will need to maintain pencilmarks while solving the puzzle. Basically, the pencilmarks indicate the possible candidate digits for each empty cell. Practically all solving strategies operate by eliminating candidates from cells until only each cell has only one candidate remaining. Cells with only one possible candidate digit can be immediately placed with that digit, in what is known as the Naked Single technique. Due to the presentation of most Sudoku programs, the givens and the placed digits are often referred to as big numbers while the pencilmarked candidates are often referred to as small numbers. The same example grid with pencilmarks is shown in the graphic below.

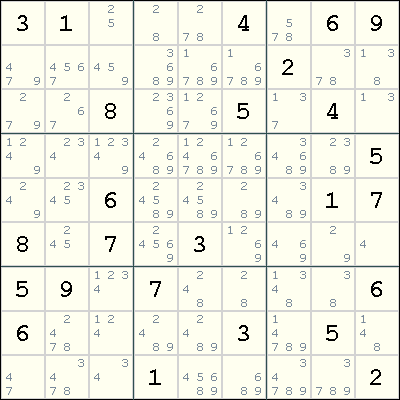
Again, for communicating in text-based forums, the text-based format for the grid with pencilmarks is shown below. It is sometimes called the candidate grid, and it has no notion of big numbers and small numbers.

.------------------------.------------------------.------------------------.
| 3       1       25     | 28      278     4      | 578     6       9      |
| 479     4567    459    | 3689    16789   16789  | 2       378     138    |
| 279     267     8      | 2369    12679   5      | 137     4       13     |
:------------------------ ------------------------ ------------------------:
| 1249    234     12349  | 24689   1246789 126789 | 34689   2389    5      |
| 249     2345    6      | 24589   24589   289    | 3489    1       7      |
| 8       245     7      | 24569   3       1269   | 469     29      4      |
:------------------------ ------------------------ ------------------------:
| 5       9       1234   | 7       248     28     | 1348    38      6      |
| 6       2478    124    | 2489    2489    3      | 14789   5       148    |
| 47      3478    34     | 1       45689   689    | 34789   3789    2      |
'------------------------'------------------------'------------------------'

Most good Sudoku programs can also import and export the textual candidate grid format.

Cell Reference

Sudoku literature often makes references to particular cells, and the preferred notation is rncn. For example, r1c2 refers to the cell at row 1 (from the top) and column 2 (from the left). This is consistent with matrix notation in mathematics.

An alternate notation that is sometimes seen is the k9 notation, which uses a letter to denote the row and a number to denote the column. However, the k9 notation often causes confusion regarding whether the letter or the number denotes the column, and whether the lettering goes from top to bottom or bottom to top. Therefore, most Sudoku literature has adopted the rncn format.

When we say that we can place a digit 3 in the cell at row 1 and column 2, we can write r1c2=3. On the other hand, when we say that the cell at row 1 and column 2 cannot contain the digit 3, or in other words, we eliminate 3 from the cell at row 1 and column 2, we can write r1c2<>3. (It appears that BASIC programmers have first propagated this notation, for the not-equals operator in BASIC is <>. Most other programming languages use != as the not-equals operator.)

Occasionally, we want to refer to groups of cells, as illustrated by the diagram below.

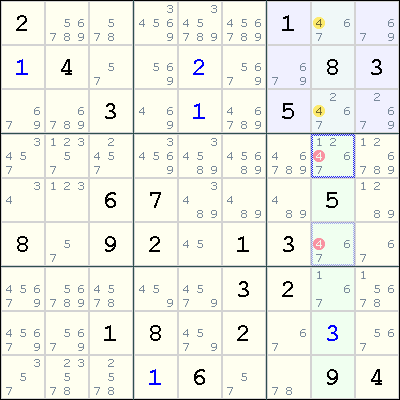
This diagram illustrates the Pointing Pair technique (click on that link for more). We want to reference both r1c8 and r3c8 (marked yellow), so we can use r13c8 to reference them. Similarly, to say that we are eliminating the digit 4 from both r4c8 and r6c8 (marked red), we can simply write r46c8<>4.

Similarly, we can write r13c24 when referring to four cells, r135c24 when referring to six cells. These are typically seen when describing deadly patterns, such as Unique Rectangles.

Eliminations

We use the Pointing Pair example again to illustrate the problem of communicating in text-based forums.

Usually, a pencilmark grid is used to describe such eliminations. Typically, a * is prefixed or appended to the cells in question to indicate the cause of the elimination, and a - is prefixed or appended to indicate the cell where the eliminations takes place. The result is shown below.

.---------------------.---------------------.---------------------.
| 2      56789  578   | 34569  345789 456789| 1     *467    679   |
| 1      4      57    | 569    2      5679  | 679    8      3     |
| 679    6789   3     | 469    1      46789 | 5     *2467   2679  |
:--------------------- --------------------- ---------------------:
| 3457   12357  2457  | 34569  34589  45689 | 46789 -12467  126789|
| 34     123    6     | 7      3489   489   | 489    5      1289  |
| 8      57     9     | 2      45     1     | 3     -467    67    |
:--------------------- --------------------- ---------------------:
| 45679  56789  4578  | 459    4579   3     | 2      167    15678 |
| 45679  5679   1     | 8      4579   2     | 67     3      567   |
| 357    23578  2578  | 1      6      57    | 78     9      4     |
'---------------------'---------------------'---------------------'

In this example, the logic behind the eliminations involves only a single digit, the digit 4. Thus some people choose to communicate the same message by showing only the cells with 4 as a candidate, like the one shown below. This kind of grid tend to be much easier to read than the grid showing the entire pencilmarks.

.---------.----------.----------.
| .  .  . |  4  4  4 |  . *4  . |
| .  .  . |  .  .  . |  .  .  . |
| .  .  . |  4  .  4 |  . *4  . |
:--------- ---------- ----------:
| 4  .  4 |  4  4  4 |  4 -4  . |
| 4  .  . |  .  4  4 |  4  .  . |
| .  .  . |  .  4  . |  . -4  . |
:--------- ---------- ----------:
| 4  .  4 |  4  4  . |  .  .  . |
| 4  .  . |  .  4  . |  .  .  . |
| .  .  . |  .  .  . |  .  .  . |
'---------'----------'----------'

Note: Beginning Sudoku players may choose to skip the remainder of this section.

In more advanced techniques such as Uniqueness Tests and Bivalue Universal Graves, more elaborate markings may be used. The following example comes from Uniqueness Test.

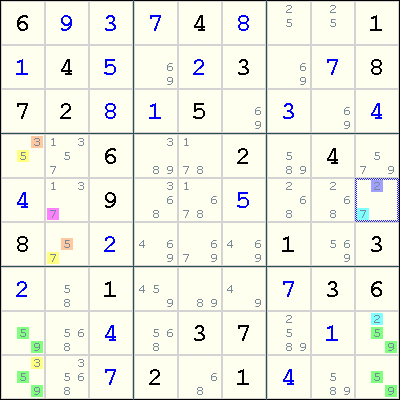
In such techniques, the + is used to indicate that the candidates after the + sign are surplus candidates. Also, sometimes the - sign is not merely prefixed or appended, but placed in the middle of the candidates. In this case, all candidates after the - sign are eliminated. The Unique Rectangle causing the elimination is marked with *.

.---------------.---------------.---------------.
| 6    9    3   | 7    4    8   | 25   25   1   |
| 1    4    5   | 69   2    3   | 69   7    8   |
| 7    2    8   | 1    5    69  | 3    69   4   |
:--------------- --------------- ---------------:
| 35   1357 6   | 389  178  2   | 589  4    579 |
| 4    13-7 9   | 368  1678 5   | 268  268  27  |
| 8    57   2   | 469  679  469 | 1    569  3   |
:--------------- --------------- ---------------:
| 2    58   1   | 459  89   49  | 7    3    6   |
|*59   568  4   | 568  3    7   | 2589 1   *59+2|
|*59 3 3568 7   | 2    68   1   | 4    589 *59  |
'---------------'---------------'---------------'

For more complex techniques where the * symbol is not sufficient to indicate the cause of the eliminations, or when illustrating multiple techniques causing multiple eliminations in a single diagram, other symbols such as # and @ can be used.

Single-digit Concept Diagrams

A number of solving techniques perform elimination based on the patterns for a particular digit, and hence called single-digit techniques. In order to highlight the concept without getting lost in the large number of candidates in a typical grid, the digit is usually generically referred to as X, and the community has also developed a kind of concept diagram. In such a diagram, each cell contains a symbol:

X

The digit X is a candidate in this cell. (It does not matter what other candidates this cell contains.)

- or /

The digit X is not a candidate in this cell.

. or no symbol

It does not matter whether this cell contains X as a candidate.

*

X can be eliminated from this cell.

Note that in such diagrams, - and * have different meanings from those seen in the pencilmark grid elimination diagrams. An example below:

.-------.-------.-------.
| X X X | * * * | * * * |
| - - - |       |       |
| - - - |       |       |
:------- ------- -------:
|       |       |       |
|       |       |       |
|       |       |       |
:------- ------- -------:
|       |       |       |
|       |       |       |
|       |       |       |
'-------'-------'-------'

This is the Pointing Triple technique, and it says that if the candidates for X in a box is confined to a row, then X can be eliminated from the cells in the row that are not in the box. (The logic is exactly the same with Pointing Pair.)

Some people choose to show such concept diagrams using an arbitrary digit instead of the symbol X. Usually, the digit 1 is used.

The fish-related techniques is a large class of single-digit techniques. Such single-digit concept diagrams have been further specialized to fish diagrams, by introducing a special symbol F for fins.

Multiple-digit Concept Diagrams

Such single-digit diagrams have been extended for multiple digits, but with an important difference. A cell may now contain multiple digits, but the semantics may mean that either the cell contains exactly these candidates as indicated, or the candidates of the cell is a subset of the indicated digits. Also, the eliminations may be for one or more digits, this will be stated in the accompanying description. For example:

.-------------.-------------.-------------.
| XYZ XYZ XYZ | *   *   *   | *   *   *   |
| *   *   *   | .   .   .   | .   .   .   |
| *   *   *   | .   .   .   | .   .   .   |
:------------- ------------- -------------:
| .   .   .   | .   .   .   | .   .   .   |
| .   .   .   | .   .   .   | .   .   .   |
| .   .   .   | .   .   .   | .   .   .   |
:------------- ------------- -------------:
| .   .   .   | .   .   .   | .   .   .   |
| .   .   .   | .   .   .   | .   .   .   |
| .   .   .   | .   .   .   | .   .   .   |
'-------------'-------------'-------------'

This diagram illustrates the Naked Triple technique. It means that if we can find a boxrow such that the candidates of each cell of the boxrow is a subset of {X, Y, Z}, then we can eliminate X, Y and Z from the remainder of the row and the box containing the boxrow.

Another example:

.-------------.-------------.-------------.
| .   .   .   | .   .   .   | .   .   .   |
| .   XY  .   | .   XZ  .   | .   .   .   |
| .   .   .   | .   .   .   | .   .   .   |
:------------- ------------- -------------:
| .   .   .   | .   .   .   | .   .   .   |
| .   YZ  .   | .   *   .   | .   .   .   |
| .   .   .   | .   .   .   | .   .   .   |
:------------- ------------- -------------:
| .   .   .   | .   .   .   | .   .   .   |
| .   .   .   | .   .   .   | .   .   .   |
| .   .   .   | .   .   .   | .   .   .   |
'-------------'-------------'-------------'

This is the XY-Wing technique, and the elimination is only for Z. Here, the three cells should contain exactly {X, Y}, {X, Z} and {Y, Z} as their respective candidates in order for this technique to be meaningful.

Chains and Loops

Note: Beginning Sudoku players may choose to skip this section.

Chains and loops are used in advanced solving techniques, and these have a set of notations. See the following articles for more information:

• Forcing Chain
• Nice Loop
• Eureka

See Also

• Terminology
• Solving techniques

This page was last modified 01:45, 19 November 2008.  

---