Mirrored from Sudopedia, the Free Sudoku Reference Guide

Uniqueness Test

The Uniqueness Tests are a set of techniques that avoid the various deadly patterns, assuming that the given Sudoku is valid. The patterns involved are often easy to recognize, but it should be noted that since a deadly pattern will never occur in a valid Sudoku, these techniques are not strictly necessary to avoid them -- the puzzle can always be solved by other means. Or so it is claimed--see Uniqueness Controversy.

This article focuses on the uniqueness tests used to avoid the Unique Rectangle deadly pattern. The techniques used to avoid the Bivalue Universal Grave (BUG) and BUG Lite patterns are discussed in the BUG and BUG Lite articles. See also the Avoidable Rectangle article.

Contents

Floor and Ceiling

Generally, the Unique Rectangle tests consider four cells that form a rectangle whose common candidates are two digits, with one or more of these cells containing extra candidates as well. The 4 cells in the corners of the rectangle belong to exactly 2 rows, 2 columns and 2 boxes. To avoid this deadly pattern, at least one of the extra candidates must be placed.

In many of the patterns for the Uniqueness Tests, two cells on one side of the rectangle (i.e., sharing either the same row or the same column) have only the common two candidate digits and no extra candidates. These cells form the floor of the rectangle. The other two cells are called the ceiling.

Uniqueness Tests

Uniqueness Test 1

Uniqueness Test 1 is the simplest among all uniqueness tests. It can be stated as follows:

If there is only one cell in the rectangle that contains extra candidates, then the common candidates can be eliminated from that cell. A rectangle that meets this test is also known as a Type 1 Unique Rectangle.

An example below:

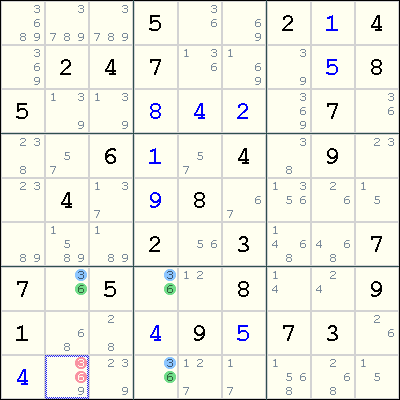
image:UniquenessTest1.png

Suppose r9c2 contains only either 3 or 6, i.e. having 3 and 6 as its only candidates. Then the four cells r7c2, r7c4, r9c4 and r9c2 forms a Unique Rectangle deadly pattern on the digits 3 and 6, which makes the puzzle invalid. Therefore, both 3 and 6 can be eliminated from r9c2.

Possible Eureka notation: 

(9)r9c2 = (36)UR:r79c24 => r9c2 = 9

As the UR must be false, (9)r9c2 must be true

Uniqueness Test 2

This test can be stated as follows:

Suppose both ceiling cells in the rectangle have exactly one extra candidate X. Then X can be eliminated from the cells seen by both of these cells. A rectangle that meets this test is also known as a Type 2 Unique Rectangle.

Note the similarity with Uniqueness Test 5 described later.

Uniqueness Test 2 can be illustrated in the example below:

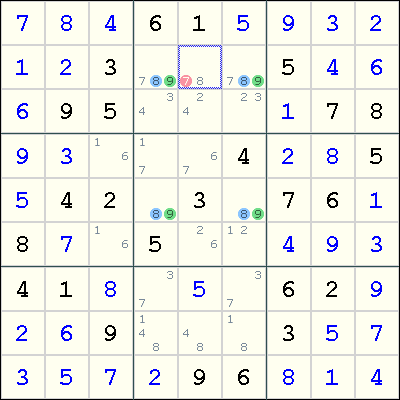
image:UniquenessTest2.png

r5c4 and r5c6 form the floor of the rectangle with r2c4 and r2c6 as the ceiling. To avoid the Unique Rectangle for the digits 8 and 9, either r2c4 or r2c6 must contain the digit 7. Therefore, 7 can be eliminated from any cell that is seen by both r2c4 and r2c6.

Possible Eureka notation: 

(8=7)r2c5 - (7)r2c46 = (89)UR:r25c45 => r2c5 = 8

As before, because the UR must be false, (8)r2c5 must be true

Uniqueness Test 3

This test can be stated as follows:

Suppose both ceiling cells have extra candidates. By treating these two cells as one node, find k - 1 other cells (as nodes) in the same house as these two cells so that the union of the candidates for these k cells has exactly k unique digits. Then the Naked Subset rule can be applied eliminate these k digits from the other cells in the house. A rectangle that meets this test is also called a Type 3 Unique Rectangle.

In a way, Uniqueness Test 3 can be seen as an extension of Uniqueness Test 2. When k = 1, Test 3 reduces to Test 2.

An example below, from the Players' forum:

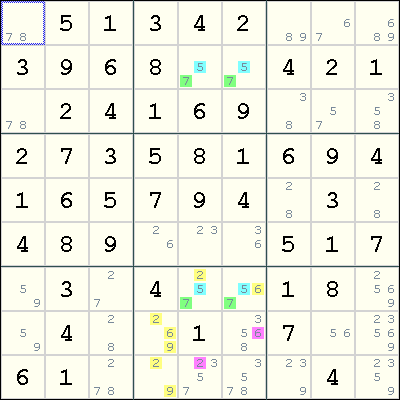
image:UniquenessTest3.png

r2c5 and r2c6 are the floor of the rectangle with r7c5 and r7c6 being the ceiling. By treating r7c56, r8c4 and r9c4 as a Naked Triple on the digits 2, 6, and 9, we can eliminate 6 from r8c6 and 2 from r9c5.

Possible Eureka notation: 

(6=92)ALS:r89c4 - (2)r7c5 =[(57)UR:r27c56]= (6)r7c6 - Loop => r8c6 <> 6, r9c5 <> 5

(2)r7c5 and (6)r7c6 can't both be false otherwise the UR is formed. There is therefore a strong inference between them. All the links in a closed loop are shown to be conjugate which provides the exclusions. Alternatively: 

(6=92)ALS:r89c4 - (2=57)ALS:r27c4 -[UR]- (57=6)ALS:r27c5 - Loop => r8c6 <> 6, r9c5 <> 5

Here the digit pair 57 is considered to be weakly linked between the UR cells in the two columns.

Uniqueness Test 4

This test can be stated as follows:

Suppose both cells in the ceiling contain extra candidates. Suppose the common candidates are U and V, and none of the cells seen by both ceiling cells contains U. Then V can be eliminated from these two cells. A rectangle that meets this test is also called a Type 4 Unique Rectangle.

An example below:

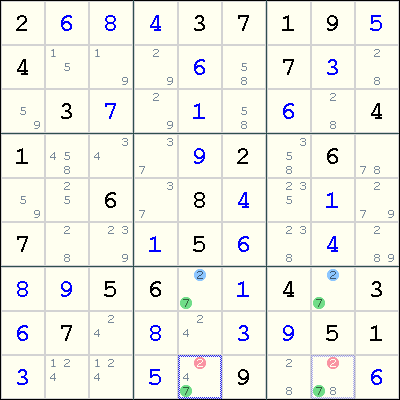
image:UniquenessTest4.png

In this example, observe that the common candidates are 2 and 7, and the extra candidates lie in the ceiling cells r9c5 and r9c8. However, in row 9, the digit 7 must be placed in either r9c5 or r9c8. Since exactly two digits must be placed in r9c5 and r9c8, one being the digit 7 and the other coming from one of the extra candidates, there is no room for these two cells to contain the digit 2. Thus, 2 can be eliminated from both r9c5 and r9c8.

Possible Eureka notation: 

(27)LockedSet:r7c58 -UR- (27)r9c58 = (2)r9c237 => r9c58 <> 2

Uniqueness Test 5

Uniqueness Test 5 is very similar to Uniqueness Test 2, and can be stated as follows:

Suppose exactly two cells in the rectangle have exactly one extra candidate X, and both cells are located diagonally across each other in the rectangle. Then X can be eliminated from the cells seen by both of these cells. This would be called a Type 5 Unique Rectangle.

Note that in this case the rectangle does not have a floor or ceiling.

The raw form of this technique appears to be extremely rare. An example:

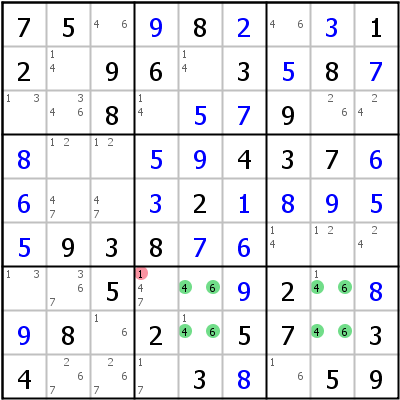
image:UniquenessTest5.png

Some players will also call the following variant as Uniqueness Test 5:

Suppose exactly three cells in the rectangle have exactly one extra candidate X. Then X can be eliminated from the cells seen by all three cells.

An example below, from the Players' forum:

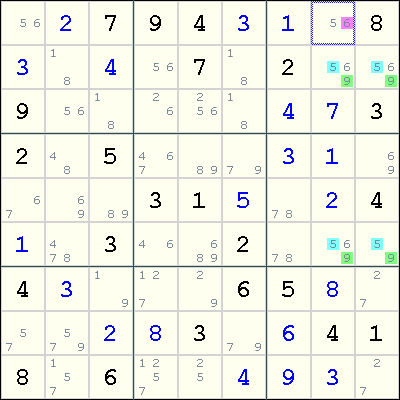
image:UniquenessTest5Variant.png

Note the unique rectangle where rows 2 and 6, and columns 8 and 9 intersect. The common candidates are 5 and 9, and three of these cells, r2c8, r2c9 and r6c8, have an extra candidate 6. To avoid the deadly pattern, at least one of r2c8, r2c9 and r6c8 must contain a 6. As r1c8 sees all of these three cells, we can eliminate 6 from r1c8.

Possible Eureka notation: 

(6)r2c89 =[(69)UR:r26c89]= (6)r26c8 => r1c8 <> 6

or: 

(6=59)ALS:r26c9 -[UR]- (59=6)ALS:r26c8 => r1c8 <> 6

Uniqueness Test 6

Uniqueness Test 6 is very similar to Uniqueness Test 4, and can be stated as follows:

Suppose exactly two cells in the rectangle contain extra candidates, and they are located diagonally across each other in the rectangle. Suppose the common candidates are U and V, and none of the other cells in the two rows and two columns containing the rectangle contain U. Then U can be eliminated from these two cells. This is also called a Type 6 Unique Rectangle.

Note that in this case the rectangle does not have a floor or ceiling.

An example below, from the Players' forum:

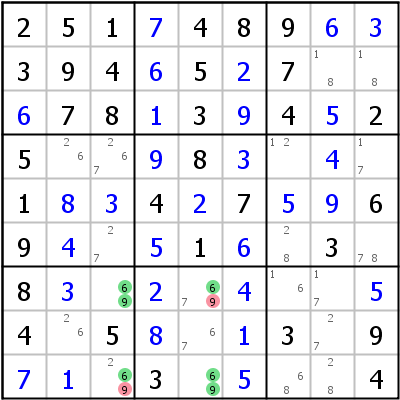
image:Uniqueness6a.png

An unique rectangle on the digits 6 and 9 plus two other candidates can be found in the intersections of rows 7 and 9, and the columns 3 and 5. In these rows and columns, the candidates for digit 9 can only be found in r7c3, r7c5, r9c5 and r9c3. Assigning 9 to either r7c5 and r9c3 forces 6 in the other corner cells to give one of the two forbidden patterns. So the digit 9 can be safely eliminated from these two cells.

Possible Eureka Notation: 

(9)r7c3 = (9-7)r7c5 =[(69)UR:r79c35]= (2)r9c3 => r9c3 <> 9

This uses the strong inference between the two disrupting digits to achieve the same effect.

Hidden Unique Rectangle

Suppose we have a rectangle with cells A, B, C, D, such that AD and BC are in opposite corners, and either AB or BD share a box, and the cells have candidates as follows: A has ab, B has abx, C has aby and D has abz, where x, y are one or more candidates, z is zero or more candidates, and the same candidate may occur in more than one of these sets. Suppose further that B and D share a house such that they are the only cells where candidate a can occur, and C and D similarly share a house where only they have a as a candidate. Then we can eliminate b from cell D.

How this works: Suppose cell D has the value b. Then both B and C must have the value a, since these cells share a house with D where they are the only other place an a can go. This means that cell A must have the value b. But since none of the four cells in the rectangle is a given, this is precisely the deadly pattern that allows for two solutions to the Sudoku--we could swap a for b in the rectangle and still have a valid solution. Therefore, b can be eliminated as a candidate for D.

Here is an example: 

.------------------.------------------.------------------.
| 135   19    6    | 24    27    247  | 8     1359  39   |
| 358   29    23   | 8     6     1    | 379   34579 3479 |
| 17    8     4    | 5     9     3    | 2     17    6    |
:------------------+------------------+------------------:
| 2     3     18   | 149   17    478  | 479   6     5    |
| 4     6     58   | 29    35    278  | 379   379   1    |
| 9     7     15   | 146   35    46   | 34    8     2    |
:------------------+------------------+------------------:
| 18    12    9    | 3     4     5    | 6     27    78   |
| 6     5     23   | 7     8     9    | 1     234   34   |
| 38    4     7    | 126   12    26   | 5     39    389  |
'------------------'------------------'------------------'

The Hidden Unique Rectangle is A=r8c9, B=r8c8, C=r2c9, D=r2c8, a=4, b=3. r2c8 and r2c9 are the only cells in r2 with candidate 4; similarly, r2c8 and r8c8 are the only cells in c8 with candidate 4. We therefore can remove candidate 3 from r2c8.

Another example from the Programmer's Forum:

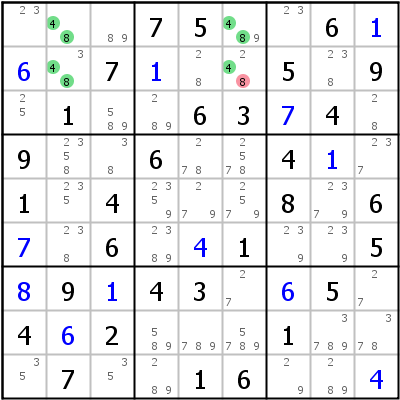
image:HiddenUR01.png

The Hidden Unique Rectangle is r1c26,r2c26, candidate 4 occurs only once in row 2 and column 6 so candidate 8 can be deleted from r2c6.

And one where z is zero candidates:

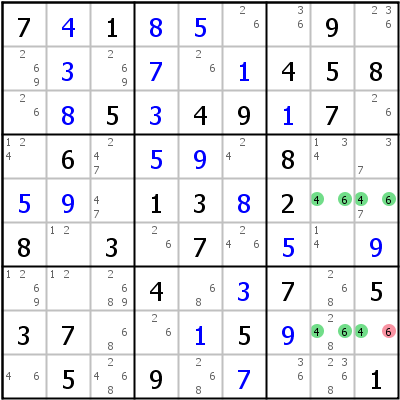
image:HiddenUR02.png

Here the Hidden Unique Rectangle is r5c89,r8c89, candidate 4 occurs only once in row 8 and column 9 so candidate 6 can be deleted from r8c9.

Unique Rectangle and Implications

Unique Rectangle and Forcing Chains

A Unique Rectangle with extra candidates means that at least one of the extra candidates must be placed in its cell. This means that each of the extra candidates can be the starting point of a Forcing Chain.

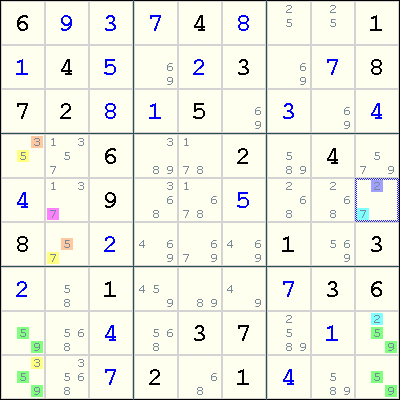
image:URStrongLink.png

In this example, since either r9c1 contains 3 or r8c9 contains 2, we can form two Forcing Chains: 

r9c1=3 => r4c1<>3 => r4c1=5 => r6c2<>5 => r6c2=7 => r5c2<>7
r8c9=2 => r5c9<>2 => r5c9=7 => r5c2<>7

Both chains result in r5c2<>7, so we can eliminate 7 from r5c2.

Unique Rectangle as Strong Link

When a Unique Rectangle has exactly two extra candidates, then the elimination of any one candidate means that the other candidate must be placed. This implies that these two candidates have a strong link. Note that this strong link does not necessarily encode a weak link, but the strong-only link may be sufficient to make an inference that causes eliminations in other cells.

image:URStrongLink.png

This is the same example as above, but recast to use a loop to make the same elimination. First, observe that we have a strong link between 3 at r9c1 and 2 at r8c9. This enables us to construct the following Alternating Inference Chain (in Eureka notation): 

(7)r5c2-(7=5)r6c2-(5=3)r4c1-(3)r9c1=(2)r8c9-(2=7)r5c9-(7)r5c2 => r5c2<>7

This also results in 7 being eliminated from r5c2.

Uniqueness Tests in Sudoku Solvers

Due to the similarity of Uniqueness Test 2, Uniqueness Test 5 and its variant, programmers of Sudoku solvers often code them as one single rule or procedure:

Suppose exactly two or three cells in the rectangle have exactly one extra candidate X. Then X can be eliminated from the cells seen by all of these cells.

Uniqueness Tests in Killer Sudoku

Uniqueness tests can be adapted to Killer Sudoku with a bit of modification on finding Unique Rectangles. For Killers, the 4 cells in the corners of the rectangle belong to exactly 2 rows, 2 columns, 2 boxes and 2 cages.

See Also

This page was last modified 15:06, 30 March 2009.