Mirrored from Sudopedia, the Free Sudoku Reference Guide

X-Chain

A X-Chain is a single-digit solving technique which uses a chain consisting of links that alternate between strong links and weak links, with the starting and ending link being strong. In other words, the chain involves an even number of cells having the target digit as a candidate. The target digit can be eliminated from any cell that is seen by both ends of the X-Chain.

The X-Chain technique and the Multi-Colors technique are equally powerful. Also, a X-Chain is also a Double Implication Chain and an Alternating Inference Chain.

Contents

Example

This is an example of a X-Chain of length six for the digit 3.

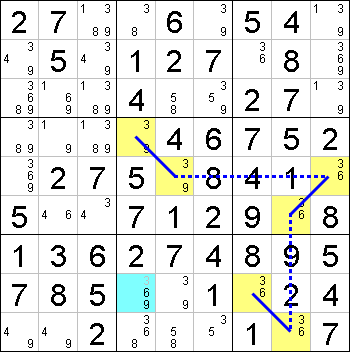
image:XChain.png

In this example, the X-Chain is marked using blue lines, with solid lines indicating strong links and dotted lines indicating weak links. In Nice Loop notation, the X-Chain can be expressed as follows: 

[r4c4]=3=[r5c5]-3-[r5c9]=3=[r6c8]-3-[r9c8]=3=[r8c7]

The two ends of the chain are r4c4 and r8c7, and either end not being 3 will result in the other end being 3. This means that r8c4, which is seen by both r4c4 and r8c7, cannot contain 3.

One proof for this is that we can formulate these two Forcing Chains, with the second due to the X-Chain: 

r4c4=3 => r8c4<>3
r4c4<>3 => r5c5=3 => r5c9<>3 => r6c8=3 => r9c8<>3 => r8c7=3 => r8c4<>3

X-Chain and Multi-Colors

X-Chain can be replicated by Multi-Colors by treating each pair of cells connected by a strong link as a color cluster and weak links as bridges between clusters. Multi-Colors can be replicated by X-Chain by the reverse of the above, and treating some of the strong links induced by the color clusters as weak links.

Minimum Length of X-Chain

In an ordinary Sudoku, the shortest useful X-Chain that allows eliminations to be made must involve at least four cells.

However, in Sudoku Variants such as Sudoku-X and Killer Sudoku, the shortest useful X-Chain can involve only two cells. An example is illustrated in the Crossover technique for Sudoku-X, made possible due to the diagonal constraints. When we eliminate candidates using a X-Chain of two cells, the same elimination can be performed using Common Peer Elimination.

See Also

This page was last modified 13:40, 3 July 2007.