---

Common Peer Elimination

Common Peer Elimination is a basic solving technique that primarily applies to Sudoku Variations with irregular groups of cells, such as Jigsaw and Killer Sudoku, and (to a lesser extent) to Sudoku-X. It is based on the following simple principle:

"If a group of cells G is known to contain the digit D, then we can remove D as a candidate from all other cells that can see all candidate positions for digit D in group G."

Note: This technique is a superset of the classical technique Locked Candidates.

Contents 1 Example 1 (Jigsaw) 2 Example 2 (Killer) 3 Notes 4 See Also

Example 1 (Jigsaw)

The following example is taken from Daily Jigsaw 13. Note that there are three possible positions for the digit 3 in column 9: r1c9, r2c9 and r4c9. All three cells have r4c7 as a common peer. Therefore, the candidate 3 can be eliminated from r4c7.

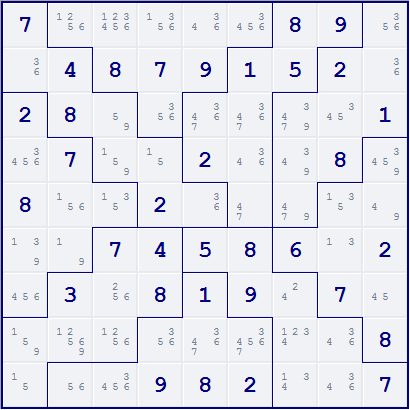
Example 2 (Killer)

The following example is taken from Weekly Assassin 36. The 27/4 cage at r2c2 must be either {5679} or {4689}, and therefore must contain the digits 6 and 9. Both cells in the 9/2 cage at r1c3 can see all cells in the 27/4 cage. Therefore, the candidate 6 can be eliminated from r12c3, which must therefore contain the digits {27}.

Notes

• If group G (see formal definition above) contains only 2 candidate positions for digit D, the same candidate eliminations can be caught by Simple Coloring.
• For Sudoku-X, Common Peer Elimination catches all simple Crossovers.

See Also

• Locked Candidates
• Simple Colors

This page was last modified 14:26, 13 May 2007.  

---