---

Swordfish

A Swordfish is a basic fish pattern with 3 rows and 3 columns. It is a single-digit solving technique.

Contents 1 Swordfish in the Rows 1.1 Example 2 Swordfish in the Columns 2.1 Example 3 Trawling for Fish Using Locked Sets 4 Practice Sudokus 5 See Also

Swordfish in the Rows

When all candidates for digit X in 3 rows are located in only 3 columns, we can eliminate all candidates for digit X from those 3 columns except those located on the defining 3 rows.

Here is a diagram that shows a Swordfish in the rows:

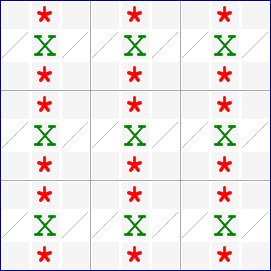
The candidates in the 3 defining rows are marked X. These candidates only occupy 3 columns. Because it is impossible to have more than one instance of a digit in a column, each instance of X in the defining rows must be placed in one of these 3 columns. In other words: the candidates for digit X in these 3 columns must be located in these 3 rows. This allows us to eliminate the remaining candidates in these 3 columns.

Each defining row can contain 2 or 3 candidates for digit X. A minimum Swordfish has a different appearance, but it still fits the definition:

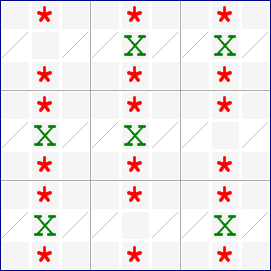
A minimum Swordfish can also be seen as a Fishy Cycle.

Example

The diagrams are useful to understand how this technique works, but as you will see in the following example, a Swordfish is not easy to spot in a pencilmark grid.

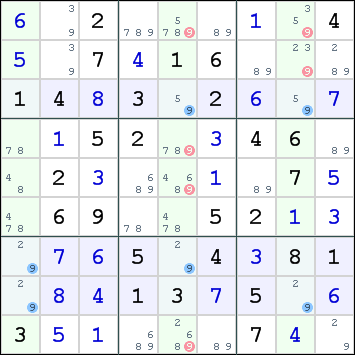
Swordfish for digit 9 in rows 3,7,8 and columns 1,5,8.

Swordfish in the Columns

When all candidates for digit X in 3 columns are located in only 3 rows, we can eliminate all candidates for digit X from those 3 rows except those located on the defining 3 columns.

Here is the diagram for this version:

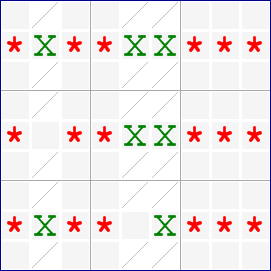
In this diagram, you can also see that is is possible to have 2 defining columns in a single chute. Two of the secondary lines can also be located in a single chute, but it is not possible to have 3 lines of a Swordfish crossing in a single box. In that case, the Swordfish would degenerate into a series of Locked Candidates.

Example

Here is an example of a Swordfish in the columns:

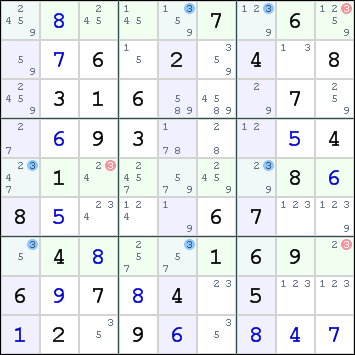
Minimum Swordfish for digit 3 in columns 1,5,7 and rows 1,5,7.

Trawling for Fish Using Locked Sets

As already pointed out, it may be difficult to spot a Swordfish in a pencilmark grid. But the analysis and discovery of basic fish (X-Wing, Swordfish, Jellyfish, Squirmbag) can be made easier by mapping the fish problem onto a Locked Set problem. See Fish and Subsets to find out how to perform this mapping.

Practice Sudokus

The following puzzles will help you practice this technique:

000308002000040700001970080905003006037000520800500903070096100006030000400807000
000000000008206900109804206004602500700000008001307400603405709005903800000000000
800060000000007600025900010008604000400000006000108300010006790002400000000090004
003105400000070000604903705501000302070030050802000907107306204000010000006207500
260907043730000089000000000100306005000070000400502001000000000340000097920403016

Select and copy each string and paste it into a computer program that accepts this input.

See Also

• Fish
• X-Wing
• Jellyfish
• Finned Swordfish
• Sashimi Swordfish
• Franken Swordfish
• Mutant Swordfish
• Fish and Subsets

This page was last modified 22:05, 12 October 2008.  

---