Mirrored from Sudopedia, the Free Sudoku Reference Guide
Franken Swordfish
The Franken Swordfish is a fish pattern of the Franken Fish type. This type allows either the defining set or the secondary set to contain boxes, as well as lines.
This is a fish diagram of a Franken Swordfish:
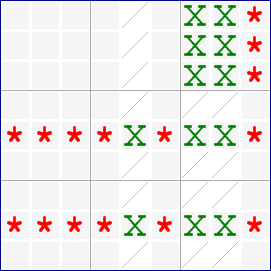
In this example, the defining set contains columns 5, 7 & 8. The secondary set contains rows 5 & 8 and box 3. All the candidates in the defining set (marked with X) are located inside the secondary set. The remaining candidates from these 3 constraints can be eliminated.
The 5 Patterns for the Franken Swordfish
The previous example is the maximum pattern for the franken swordfish. It contains 12 cells and because of this its occurence is much rarer than the any of the other 4 patterns. Logical analysis of the minimum pattern shows that 4 of the cells in box 3 of the example are redundant. The other 4 patterns occur when 1, 2, 3, 4 of these redundant cells are removed. The only restriction on this is there must be at least 1 cell in each of the box 3 columns in the pattern. The minimum pattern occurs when there is only 1 cell in each of columns 7 and 8 of box 3. Since there are 9 different ways these cells can occur. The probability of occurence is 9 times that of the maximum pattern. There is nothing finnish or sashimish about any of the 5 patterns. In a finned or sashimi row or column swordfish cell eliminations occur only in the box with the fin. In contrast the 5 franken swordfish patterns with 8 through 12 cells all give exactly the same cell eliminations. They are analogous to the 4 patterns of the row or column swordfish with 6, 7, 8 and 9 cells. Because of the 5 patterns of the franken swordfish, the probobility of occurence may be comparable to that of the row or column swordfish.
The diagram of a minimum franken swordfish pattern is shown below.
How It Works.
Since A and B are conjugate pairs either A exclusive or B is X. If A is X none of the peer cells in row 5 can be X. This creates 2 conditional conjugate pairs (EG and FH) in columns 7 and 8. Since G and H are peers and E and F are peers, one and only 1 of each of the peer groups must be X. Therefore X can be no additional X's in row 7 are box 3. If B is X none of the peer cells in row 7 can be X. This creates 2 conditional conjugate pairs (CG and DH) in columns 7 and 8. Since G and H are peers and C and D are peers, one and only 1 of each of the peer groups must be X. Therefore X can be no additional X's in row 5 are box 3. QED
The logic for the other 4 patterns is similar except that one or both of the conditional conjugate pairs become conditional group conjugates. The logic is still valid for this case.
A Combined Franken/Column Swordfish
It is possible to have an 8 cell pattern which is both a franken swordfish and a column(row) swordfish. In this case additional cell eliminations can be made. An example of this is shown in the diagram below.
It is also possible to have a 9 cell pattern which is both a franken swordfish and a finned column(row) swordfish. In this case the finned swordfish pattern does not provide any additional cell eliminations. An example of this is shown in the diagram below.
A Finned Franken Swordfish Example
Here is example of a finned franken swordfish. The fin in this example occurs in box 5 and the only cell eliminations for this pattern are also in box 5.
See Also
This page was last modified 21:48, 30 December 2009.

