Mirrored from Sudopedia, the Free Sudoku Reference Guide

Fish and Subsets

Fish and Subsets are complementary to each other. One can transform a problem of finding a fish into a problem of finding a subset, and vice versa.

Trawling for Fish Using Locked Sets

It may be difficult to spot a fish in a pencilmark grid, especially Swordfish, Jellyfish, or Squirmbags. But the analysis and discovery of basic fish (X-Wing, Swordfish, Jellyfish, Squirmbag) can be made easier by mapping the fish problem onto a Locked Set problem. Here is the procedure for analyzing a row-based Swordfish:

Make a list of 9 sets, each one corresponding to a row in the Sudoku. Populate each set with the column numbers of each column within that row that has the digit for which we're searching for a basic fish.
Examine the sets, looking for a locked triple--a group of three sets containing only the same three numbers.
If you find such a locked triple, you have netted a Swordfish! The digits in the locked triple are the column numbers in the Swordfish.

For a column-based Swordfish, swap "row" and "column" in the procedure:

Make a list of 9 sets, each one corresponding to a column in the Sudoku. Populate each set with the row numbers of each row within that column that has the digit for which we're searching for a basic fish.
Examine the sets, looking for a locked triple--a group of three sets containing only the same three numbers.
If you find such a locked triple, you have netted a Swordfish! The digits in the locked triple are the row numbers in the Swordfish.

This technique also applies to the other basic fish: X-Wing, Jellyfish, and Squirmbag. In these cases, one looks for a locked pair, locked quadruple, or locked quintuple, respectively.

Example

Here we apply this technique to the "Swordfish in the Columns" example below to search for a swordfish on digit 3.

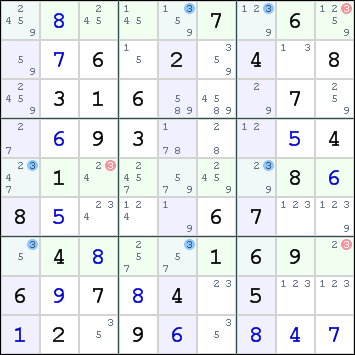
image:Swordfish-crx.png

The sets of row numbers are:

1:{57} 2:{} 3:{569} 4:{} 5:{17} 6:{289} 7:{15} 8:{268} 9:{1678}

Sets 1, 5, and 7 form the locked triple {57}, {17}, {15}. Our Swordfish is thus in columns 1,5,7 and the rows are the members of the locked triple: rows 1,5,7. The sets also point out the eliminations--they are any occurrences of the members of the locked triple in sets not part of the triple. In this case set 3 contains 5, which means digit 3 can be eliminated from cell r5c3. Similarly, 1 and 7 occur in set 9, so we can eliminate digit 3 from cells r1c9 and r7c9.

Finding a Subset by Fishing

Here is a candidate grid:

.------------------.------------------.------------------.
| 67    469   3    | 4678  5     267  | 1     789   279  |
| 57    8     2479 | 147   47    127  | 2347  6     23579|
| 1567  146   2467 | 3     4678  9    | 2478  78    257  |
:------------------+------------------+------------------:
| 4     356   8    | 67    367   3567 | 9     2     1    |
| 9     1356  567  | 168   2     1356 | 3678  378   4    |
| 1367  2     67   | 14689 34689 136  | 3678  5     367  |
:------------------+------------------+------------------:
| 8     369   1    | 2     3679  4    | 5     379   3679 |
| 36    7     69   | 5     1     8    | 236   4     2369 |
| 2     34569 4569 | 679   3679  367  | 367   1     8    |
'------------------'------------------'------------------'

Now let's focus our attention to row 6:

1367 2 67 14689 34689 136 3678 5 367

We can explode this row into a grid where the X-axis is the digit and the Y-axis is the cell. An X is placed for each candidate:

   1  2  3  4  5  6  7  8  9
1  X     X        X  X
2     X
3                 X  X
4  X        X     X     X  X
5        X  X     X     X  X
6  X     X        X
7        X        X  X  X
8              X
9        X        X  X

It is now possible to draw 2 vertical lines which intersect with only 2 horizontal lines:

   1  2  3  4  5  6  7  8  9
1  X     X  |     X  X     |
2     X     |              |
3           |     X  X     |
4  X        X     X     X  X
5        X  X     X     X  X
6  X     X  |     X        |
7        X  |     X  X  X  |
8           |  X           |
9        X  |     X  X     |

Since the candidates on these 2 vertical lines fully saturate these 2 horizontal lines, we can remove the remaining candidates from these 2 horizontal lines:

   1  2  3  4  5  6  7  8  9
1  X     X  |     X  X     |
2     X     |              |
3           |     X  X     |
4  -        X     -     -  X
5        -  X     -     -  X
6  X     X  |     X        |
7        X  |     X  X  X  |
8           |  X           |
9        X  |     X  X     |

This is the resulting candidate list for row 6:

1367 2 67 49 49 136 3678 5 367

By temporarily transforming the data, we have found a Hidden Pair using the X-Wing technique.

Extended Sudoku Board

A fish of any size appears as a naked subset in the rn- or cn- representations. These representations are dual to the usual rc- representation. They are based on the generalised logical symmetries of Sudoku. In the book "The Hidden Logic of Sudoku", an extended Sudoku board has been defined in order to facilitate a wider use of these symmetries (This extended board and the way to use it are available online: see section "External links").

The rn- and cn- representations are now also available in the Sudocue program.

Moreover, the above logical symmetries can be extended much beyond subsets and fish. For instance, the rn- and cn- representations can also be used for finding hidden chains (hidden xy, xyt, ...)

External Link

A new view of fish

Extended Sudoku Board: [1]