Mirrored from Sudopedia, the Free Sudoku Reference Guide

Sashimi Jellyfish

A Sashimi Jellyfish is a fish pattern, formed by an incomplete Jellyfish which is stabilized by additional candidates in a box that intersects with one or more lines of the defining set. It is a single-digit solving technique.

Here is a fish diagram that shows a Sashimi Jellyfish in the columns:

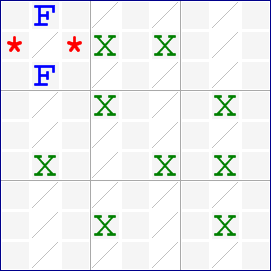
image:Sashimi_jellyfish_cr.png

The candidates marked X form an incomplete Jellyfish pattern, with 4 columns having candidates in only 4 rows. This pattern would not be stable with only a single candidate in column 2 if the 2 candidates marked F were not present. These candidates are the fin. Either one of the F candidates is true, or the Jellyfish degenerates into a single in r6c2 and a Swordfish in the remaining 3 columns. The candidates marked * are removed in both cases, allowing us to eliminate them from the grid.

Example

.------------------------.------------------------.------------------------.
| 2       9       7      | 146     3       146    | 5       *46     8      |
| 35      4       6      | 8       X257    9      | F237    M1      F37    |
| 358     358     1      | 2456    567     24567  | 379     *24679  34679  |
:------------------------ ------------------------ ------------------------:
| 9       2       3      | 45      8       X457   | 6       X57     1      |
| 457     1       45     | 256     569     256    | 379     8       379    |
| 6       X57     8      | 1359    X179    X1357  | 4       X579    2      |
:------------------------ ------------------------ ------------------------:
| 378     378     49     | 123569  1569    12356  | 179     2469    4679   |
| 45      6       459    | 7       12      8      | 12      3       49     |
| 1       X37     2      | 369     4       36     | 8       X679    5      |
'------------------------'------------------------'------------------------'

This grid contains a Sashimi Jellyfish for digit 7 in rows 2, 4, 6, and 9. The participating columns are 2, 5, 6, and 8. Cells marked with X are the vertices of the Jellyfish. But the pattern is incomplete. A pure Jellyfish would have 7 as a candidate in r2c8 (the cell marked M) and could not have 7s in r2c7 and r2c9 (the cells marked F). A Finned Jellyfish would have 7 as a candidate in both F cells and the M cell. But the fins F can "stand in" for the missing 7 in M in the sense that the same eliminations as a pure Finned Jellyfish still can be performed (this is the Sashimi Observation). 7 thus can be eliminated from r1c8 and r3c8 (the two cells marked *). In this case, only one elimination is possible: 7 from r3c8.

Considerations

A pure Sashimi Jellyfish is hard to find. Several vertices need to be removed to form an incomplete Jellyfish. The pattern you see in the diagram is only one of the ways to reduce the Jellyfish. However, other reductions often lead to alternative eliminations, which are easier to spot than the Sashimi Jellyfish.

Sashimi Jellyfish

Example

Considerations

See Also