---

Graded Equivalence Marks

From time to time, people come up with powerful solving techniques, which only receive a cool welcome by the general Sudoku community and disappear into oblivion after their inventors have given up their struggle to defend it. Graded Equivalence Marks could easily have fallen into this category if it were not for David P Bird, who has repeatedly proven the power of this technique. Yet, there is but a small group of people who actually use it. Maybe this article in Sudopedia will convince other players by showing how this simple-yet-powerful solving technique can complement their current solving toolkit.

Graded Equivalence Marks or GEM is an extension to Equivalence Marks. You should read the article and make sure you understand the concepts before you proceed with the graded version. Other prerequisite knowledge includes strong links & weak links, clusters and parity.

GEM uses 6 different markers to reveal the implications of both choices in an initial bivalue or bilocal situation. The 2 first-grade markers are the same you would use in Equivalence Marks and the process to apply them is similar to 3D Medusa coloring on a single cluster. The 4 second-grade markers are only used in GEM.

Since GEM is basically a dual implication network, it is bifurcative in nature, which acts as a repellant to many Sudoku players. Yet, when a player simply carries out the instructions, it is no more bifurcative than any other coloring technique, which also starts with a single conjugate pair.

Contents 1 Markers 2 Initial Markup 3 Marking Opposites 4 Marking Equivalents 5 Promotions and Exclusions 6 Marking Tips 7 Example

Markers

' Par marker for parity 1
" Par marker for parity 2

The par markers are the same as used in Equivalence Marks. They represent the opposite parities in the initial cluster. The parities are mutually exclusive. One must be true and the other must be false.

- Super marker for parity 1
= Super marker for parity 2

The super markers are true when the par markers for their parity are true. When their parity is false, their state is indeterminate.

. Sub marker for parity 1
: Sub marker for parity 2

The sub markers are false when the par markers for their parity are false. When their parity is true, their state is indeterminate.

Initial Markup

The usual choice of seed candidates is a bivalue cell or a bilocal digit, where the two exclusively possible candidates given opposite par marks. Less frequently other seeding options are available, for example which of two box/line intersections will hold a digit, where only sub markers may be possible, but always the basis of a mark-up must be two mutually exclusive conditions.

The method will show either a) which one of the starting conditions must be true, and/or b) which individual candidates must be false under either condition. Seed candidates should be chosen which are hoped will give the maximum return, and time spent considering the best choice is worthwhile, as a complete mark-up is time consuming.

Marking Opposites

As soon as a par or super mark has been given to a candidate, sister and cell mate candidates can be given complementary marks of the opposite parity for the type of link involved:

Complementary Marks:
Par Grade:    Strong Link:  Par  <=>  Par   ( ' + "  &  " + ' )
              Weak Link:    Par   ->  Sub   ( ' + :  &  " + . )  
Super Grade:  All links:    Super ->  Sub   ( - + :  &  = + . )     
Sub Grade:    Strong link:  Sub  <=>  Super ( . + =  &  : + - )   
                    

Sub Grade Groups: When all but one of a set of candidates carry the same sub parity, the final one may be marked with the complementary super mark. For example, a cell marked 1:5:79: would become 1:5:7-9: It should be noted that using such inferences are a cause of contention with bifurcation purists as the grouped marks often stem from different forks being followed. If this is a concern, use this condition as an indicator that a recognised pattern, such as an ALS, may exist which will achieve the same effect.

Marking Equivalents

Normally parity marking chains follow an alternating parity sequence, but sometimes it is possible to mark cells which must be equivalent to one or more marked cells. This happens when it is known that one of the three cells in a line/box intersection must eventually contain a particular par or super parity mark when all candidates in sight of the full trio can be marked accordingly.

Promotions and Exclusions

• When all but one cell mates or sisters to a par marked candidate have been excluded, the survivor can be promoted to a par mark.
• A super grade candidate seeing a par marked sister or cell mate is promoted to a par mark.
• A sub marked candidate seeing a sister or cell mate carrying a par or super grade mark of the same parity is false.
• Two candidates with opposite parity par marks in the same cell make all other candidates in that cell false.
• In a cell when all surviving cell mates have the same parity that parity is true.
• In a unit, if all sisters of a digit carry the same sub parity, the opposite parity is false.
• If two sisters or cell mates carry any combination of super and par marks for the same parity, that parity is false.

Note: when a parity is found to be false, only par and sub marked candidates for that parity are excluded, not the super grade candidates.

Marking Tips

Just as with other methods, the speed at which deductions arrive will depend on the marking order used. Quick results on easy puzzles often come from just marking the par grades first before extending the scheme to sub and super grades. Then for moderately rated puzzles, a hare approach which restricts the marking to certain groups of units holding a potentially useful reduction may be best, but for extreme puzzles, the tortoise method of taking each digit in turn and marking it to exhaustion, can avoid key inferences being missed. Often the casual eliminations made en route will be insignificant to the solution, but it is worth checking to see if they create naked pairs or box/line reductions which can be acted on first before resuming the mark-up.

Example

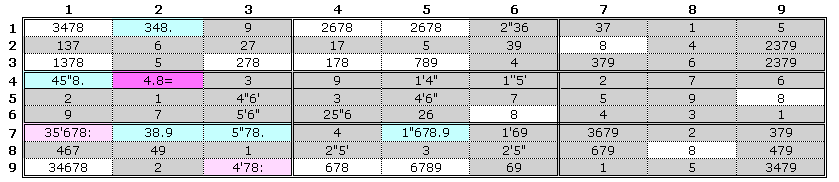
Here the marking was started from r5c5 and was restricted initially to par marks only. To avoid over-complicating the figure, super and sub grade marks have been started just for the 8s as shown by the coloring. At r4c2 the 8 is conjugate to (8.)r4c1 and so is marked (8=) from which we get (8.)r17c2. At the stage reached in the figure, (8:)r7c1 is the only 8 in the row with a parity(ii) mark so it can be promoted. Because of the existing par 5', it becomes (5'8") so excluding 3,6 & 7 there. This will also exclude the (8:) at r9c3 so the cell becomes (4'7") with the 7 being promoted. On grade marking the 7s it will then be found that box 8 cannot hold a 7 at parity(ii), so parity(i) is true which resolves 10 cells.

This page was last modified 15:55, 2 February 2007.  

---