Mirrored from Sudopedia, the Free Sudoku Reference Guide
2-String Kite
The 2-String Kite solving technique describes a particular type of Turbot Fish as a pattern.
It has been introduced as a separate technique, because the Turbot Fish technique does not use a single pattern and is not easy to learn by the average Sudoku player.
Contents |
How it works
The pattern contains 2 conjugate pairs for a single digit. One is located in a row, the other in a column. These are the 2 "strings", which are linked in a single box, representing the "kite". A candidate for this digit can be eliminated from the cell that can see both ends of the 2 strings.
Here is a diagram that shows the pattern:
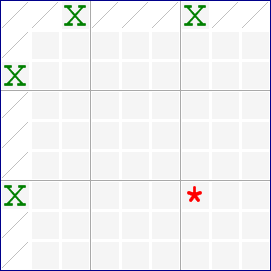
The strings are in row 1 and column 1, they meet in box 1. The candidate in r7c7 can be eliminated.
The complete loop, including the candidate in r7c7, is a Turbot Fish. It can also be written as a chain:
(X): r7c7-r7c1=r3c1-r1c3=r1c7-r7c7 => r7c7<>X
Example
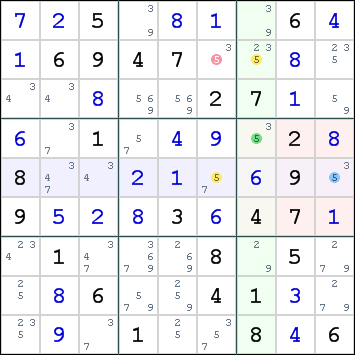
Although the candidates in box 6 have a strong link, we only use the weak inference for this technique, as shown in the following chain:
(5): r2c6-r2c7=r4c7-r5c9=r5c6-r2c6 => r2c6<>5
Not 2-String Kite
Note that the cells in both of the conjugate pairs must be in different boxes, and the cell that each line has in the box must be distinct. The example below shows what happens when two of the cells from one pair are both in the same box. The pattern degenerates into a line-box interaction (col2/box1) and a single (r1c6). The single in r1c6 still eliminates the * candidiate, but the pattern is not best described as a two-string kite.
--X|--X|--- .X.|...|... .X.|..*|... ---+---+--- .-.|...|... .-.|...|... .-.|...|... ---+---+--- .-.|...|... .-.|...|... .-.|...|...
When the cells that each line has in the box are not distinct, this is what results:
-X-|-X-|--- .-.|...|... .-.|...|... ---+---+--- .-.|...|... .X.|...|... .-.|...|... ---+---+--- .-.|...|... .-.|...|... .-.|...|...
This pattern doesn't result in any eliminations at all.
Grouped 2-String Kite
With a slightly altered definition, this pattern can also be used when there are more than 2 candidates in the strings.
Consider the candidates for a selected digit. When you can find a row and a column that do not have a candidate in their common cell, and both have only a single candidate outside the box where they meet, you can eliminate the candidate from the cell that can see both these candidates outside the shared box. The complete pattern forms a rectangle.
Here is the diagram for the grouped 2-String Kite:
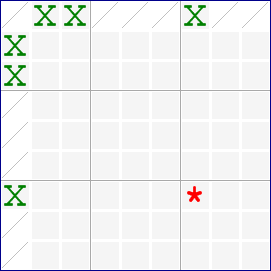
The chain for this grouped version does not differ much from the original:
(X): r7c7-r7c1=r32c1-r1c23=r1c7-r7c7 => r7c7<>X
Note
2-String Kite can be replicated using Multi-Colors.
An Extended Form of the 2-String Kite
The diagram below shows an example of an extended form of the 2-string kite which can result in 1 or 2 additional candidate cell eliminations. In order to use this technique a 2-string kite pattern must be present and 1 or 2 additional conjugate pairs must be present with one cell which is a peer of either string end of the 2-string kite. In this example the 2-string kite consists of the conjugate pairs AB and CD. The two additional conjugate pairs are EF and EG where E is a peer of B.
.-------.-------.-------. | - - A | - - - | B - - | | - . . | . . . | . . . | | C . . | . . . | . . . | :-------+-------+-------: | - - - | - F - | E - - | | - . . | . . . | - - - | | - . . | . . . | - - G | :-------+-------+-------: | D . . | . * . | * . * | | - . . | . . . | . . . | | - . . | . . . | . . . | '-------'-------'-------'
How it works. Since A and B are peers, at most only one of them can be X. Therefore either or both of their conjugates C and D must be X. If D is X, then r7c579 cannot be X. If D is not X, then B is X and its peer E is not X. Therefore both of E's conjugates G and F must also be X. Therefore r7c579 cannot be X. This extended technique can also be used with the ER technique. This is an also an example of multicoloring with 3 color chains.
Practice
The following is a practice puzzle for 2-String Kite and Skyscraper. The other techniques that are required are SSTS minus the coloring techniques. It is generated by Simple Sudoku.
000400100000705032032000700001080605070000020503010800008000560650803000007001000
