Mirrored from Sudopedia, the Free Sudoku Reference Guide

Sue de Coq

The Sue de Coq technique uses two intersecting sets A and B, where A is a set of N cells with N candidates in a line, B is a set of N cells with N candidates in a box, and the sets A - B and B - A have no common candidates. Candidates can be eliminated from the cells in the line that are not in A, and the cells in the box that are not in B.

This technique was introduced by a member using the alias Sue de Coq in the Sudoku Players' forum, who named it Two-Sector Disjoint Subsets, but a remark that this was a true Sue de Coq gave the technique its present name.

This technique can be extended into Three-Sector Disjoint Subsets, but this extension is very rarely seen.

Contents

Example

The following image shows an example of the Sue de Coq technique:

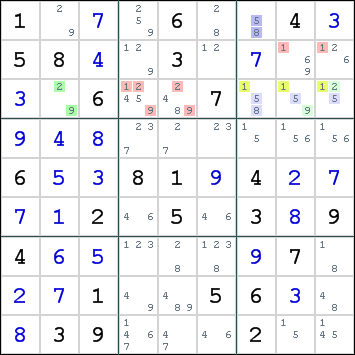
image:Sue_de_coq.png

Consider the intersection of row 3 and box 3. It has candidates 1,2,5,8,9. It cannot contain both 2 and 9 as this would conflict with r3c2. It cannot contain both 5 and 8 as this would conflict with r1c7. The intersection must contain 1 + (2 or 9) + (5 or 8). This allows us to eliminate candidates for digit 1 from row 3 and box 3, candidates for digit 2 and 9 from the remainder of row 3 and candidates for digits 5 and 8 from the remainder of box 3 (if there were any). These eliminations are shown in red.

Sue de Coq is both an elegant and effective technique, often causing several eliminations. Despite this, the technique is not often used.

Note

Sue de Coq is a special case of Subset Counting.

External Links

See Also

This page was last modified 10:14, 20 April 2009.