Mirrored from Sudopedia, the Free Sudoku Reference Guide

Dancing Links

The Dancing Links algorithm has been created by Donald Knuth to solve CSP's (Constraint Satisfaction Problems).

It can easily be adapted to function as a backtracking algorithm to solve sudokus.

Contents

Data Structures

This section describes the data structures you need in order to implement a Dancing Links solver in a Sudoku program.

Doubly-Linked List

A doubly-linked list is a list of nodes where each node has links to its predecessor and its successor in the list. The last node and the first node also have reciprocal links, turning the list into a loop or doubly-circularly-linked list. The list can be navigated in both directions by following the links. 

class node
{
  node prev;
  node next;
}

To start a list, you need a root node. When the root does not contain data, we also call this a dummy or a sentinel node. This node links to itself in both directions. The following code fragment initializes the root node: 

node root;
root.next = root;
root.prev = root;

Inserting a node at the end of the list is quite simple. Since the list is cyclic, we can insert the new node before the root with the following code: 

node Insert(node root)
{
  node newnode;
  newnode.next = root;
  newnode.prev = root.prev;
  newnode.next.prev = newnode;
  newnode.prev.next = newnode;
  return newnode;
}

To remove a node from the list, we need to update the links of its predecessor and successor. When the node does not need to remember its previous position in the list, the links of the removed node are also cleared. 

void Remove(node remnode) 
{
  remnode.next.prev = remnode.prev;
  remnode.prev.next = remnode.next;
  remnode.next = NULL;
  remnode.prev = NULL;
}

When we remove a node from the list with the intent to insert it back at the same position, the links of the removed node are not cleared, so the node remembers its position in the list. It is is important to ensure that the links of the predecessor and successor are correctly restored before reinserting it, otherwise the results will be unpredictable. 

void Cloak(node remnode) 
{
  remnode.next.prev = remnode.prev;
  remnode.prev.next = remnode.next;
}

void Uncloak(node remnode) 
{
  remnode.next.prev = remnode;
  remnode.prev.next = remnode;
}

To navigate the list, we can simply follow the links. The following code fragment traverses the list in forward direction. Please note that the start node is not handled inside the loop, because the stop condition is tested at the beginning of each iteration. 

for(node curnode = startnode.next;curnode != startnode;curnode = curnode.next)
{
  // use curnode
}

CSP Matrix

In a Constraint Satisfaction Problem or CSP, we can use a matrix of nodes forming doubly linked lists in each row and column to represent the current state of the solving process. In such a matrix, each row represents a candidate which could be part of the solution. Each column represents a constraint, with a column header node keeping track of the state of the column. The nodes in the matrix connect the candidates to the constraints which they could satisfy.

To be able to participate in 2 doubly-linked lists and to be able to access the header, we need to expand the node definition a little: 

class node
{
  node up;     //prev in column
  node down;   //next in column
  node left;   //prev in row
  node right;  //next in row
  header head; //column header of this node
}
class header : node
{
  int size;    //number of nodes linked in to the column header
}

A complete matrix, with 3 candidates participating in 4 constraints, is represented by the following diagram:

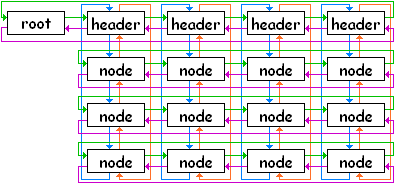
image:Dlx_matrix.png

To initialize this matrix, you need initialization functions for the root, the headers and the detail nodes: 

node CreateRoot()
{
  node root;
  root.left = root;
  root.right = root;
  return root;
}
header CreateHeader(node root)
{
  header head;
  head.right = root;
  head.left = root.left;
  head.right.left = head;
  head.left.right = head;
  head.up = head;
  head.down = head;
  head.size = 0;
  return head;
}
node CreateDetail(node last, header head)
{
  node newnode;
  if (last != NULL)
  {
    newnode.left = last;
    newnode.right = last.right;
    newnode.left.right = newnode;
    newnode.right.left = newnode;
  }
  else
  {
    newnode.left = newnode;
    newnode.right = newnode;
  }
  newnode.head = head;
  head.size++;
  newnode.down = head;
  newnode.up = head.up;
  newnode.up.down = newnode;
  newnode.down.up = newnode;
  return newnode;
}

When you create the first detail node in a row, the first parameter must be a NULL value. Subsequent nodes for the same row should be created with the last created node in this parameter.

Because the links between the nodes are constantly updated, we need to ensure that there are permanent links to each node to prevent them from being destroyed. Also, direct access to the rows and columns in the matrix may be necessary at some point. We can use two arrays to provide direct access to each row and each column. 

header columns[width];
node rows[height];

Note: rows and columns in DLX are not the same as rows and columns in a Sudoku puzzle.

Basic Methods

To bring the matrix in the initial state of the puzzle, we need to disable all rows that cannot be part of the solution. In a Sudoku puzzle, the givens must belong to the solution, allowing us to disable all other candidates in these cells. Here are the methods to disable and enable an entire row: 

void Disable(int rowIndex)
{
  node curNode = rows[rowIndex];
  do
  {
    if (curNode.down != curNode) // prevent disabling the same node twice
    {
      curNode.down.up = curNode.up;
      curNode.up.down = curNode.down;
      curNode.down = curNode;
      curNode.up = curNode;
      curNode.head.size--;       // decrement the size of the column header
    }
    curNode = curNode.right;
  }
  while (curNode != rows[rowIndex]);
}

void Enable(int rowIndex)
{
  node curNode = rows[rowIndex];
  do
  {
    if (curNode.down == curNode) // prevent enabling the same node twice
    {
      curNode.down = curNode.head;
      curNode.up = curNode.head.up;
      curNode.down.up = curNode;
      curNode.up.down = curNode;
      curNode.head.size++;       // increment the size of the column header
    }
    curNode = curNode.right;
  }
  while (curNode != rows[rowIndex]);
}

Because the nodes are always inserted before the column header when enabled, the order of the nodes in each column will have changed after the solver has been executed. The effectiveness of the solver is not impeded by this change.

Sudoku Solver Implementation

There are 4 types of constraints in Sudoku:

A total of 324 constraints need to be satisfied.

There are 729 candidates to start with in a sudoku. (81 cells x 9 digits).

The constraints and candidates will now be used as the X and Y axes of a matrix. Positions in the matrix will either be empty, or filled with a node that connects a candidate to a constraint.

Each of the 729 candidates 'competes' in 4 constraints. A total of 2916 nodes are placed in the matrix. With 324 constraints on the other axis, there are 9 nodes for each constraint (9 x 324 = 2916).

The 4 nodes of a candidate are connected with a double linked list.

The 9 nodes of a constraint are connected with a double linked list. An extra header node is added to this list. It represents the constraint. The header nodes also have a size property, that indicates how many candidates are left in the constraint. All header nodes are linked together to form another double linked list. This list finds its origin in a root node.

Basic Methods

Disable a candidate. This method removes a candidate by removing all 4 nodes from their constraint linked lists. The size of the 4 headers is also decremented.

Cover a constraint. This method removes the constraint from the linked list of all constraints.

Uncover a constraint. This method reverses the cover method.

Loading a Sudoku

The matrix is reset to the initial state. For each given digit, the other 8 candidates for the same cell are disabled.

The Recursive Process

Find the smallest constraint (call it constraint X). When the root node is the only node left, a solution is found. Cover constraint X.

Process each candidate in the linked list of constraint X.

External Links

This page was last modified 00:43, 15 April 2009.