---

Color Wrap

Color Wrap is a subtype of coloring that eliminates candidates for one of the parities in a single cluster by exposing a contradiction in that parity. The candidates with the opposite parity can be placed in their respective cells, making this a placement technique, rather than an elimination technique.

Color Wrap belongs to Simple Colors, together with Color Trap.

Every coloring move can easily be replicated by a chain. However, colors are easier to use by most players, because it is a more visual technique.

Here is an example:

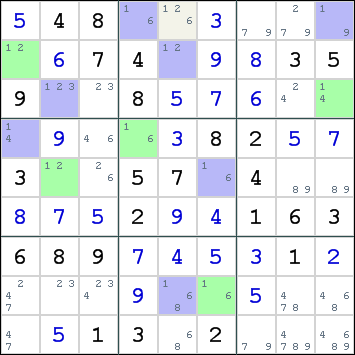
All the candidates for digit 1 are highlighted. All but one of them belong to a large cluster of conjugate pairs. The 2 parities in this cluster have the colors green and blue. All candidates with the same color are equivalent, which means that they either all contain digit 1 or none of them contains digit 1. In other words: they are true or false as a group.

In the example, it is impossible for the blue candidates to be true together, because that would cause conflicts in row 1, column 5 and box 2. The only remaining alternative is that all green colors are true. We can place digit 1 in all the green cells.

A Group Color Wrap

With simple coloring all of the links of the color chain must be conjugate pairs. With group coloring group conjugates are also allowed. There is nothing new about group conjugates. They occur in the patterns of the Finned and Sashimi X-wings. The diagram below shows the simplest example of a group color wrap. The color chain consists of 3 group conjugates in row 1, box 1, and column 2 and a conjugate pair in row 5. Note that the cells in a group must be in the same box. To understand the logical properties of a group conjugate, consider the cells in row 1. If the blue cell is X, then both red cells in the group are not X and if the blue cell is not X then one of the red cells must be X. You don't know which one, but then you don't have to know for this technique to work. Next consider the group conjugates in Box 1. If one of the blue cells is X then both of the red cells are not X and vice versa. Note that the logical properties of group conjgates are intermediate in strength between that of conjugate pairs and that of peer pairs. Although this may not look like a color chain to some, the color chain is there but the diagonal link in box 1 is fuzzy. In this example a blue color wrap occurs in column 6. This means that all of the blue cells are not X and the red cell in row 5 is X, but you still don't know which of the red cells in row 1 is X. A group color trap example is forthcoming.

X	-	X	-	-	X	-	-	-
-	X	-
-	X	-
	-			.
-	X	-	-	-	X	-	-	-
	-			.
	-
	-
	-

This page was last modified 23:55, 20 August 2008.  

---