Mirrored from Sudopedia, the Free Sudoku Reference Guide

ALS-XY-Wing

The ALS-XY-Wing rule is a solving technique that uses three Almost Locked Sets.

Make sure you understand the concept of Almost Locked Sets (ALSs) before you proceed.

How it works

Say we have three Almost Locked Sets A, B and C. Suppose

A and C share a restricted common Y,
B and C share a restricted common Z, and
Y and Z are different digits.

Then for any digit X that is distinct from Y and Z and is a common candidate for A and B, we can eliminate X from any cell that sees all cells belonging to either A or B and having X as a candidate.

Relations to other techniques

Observe that this technique generalizes XY-Wing, and hence the name ALS-XY-Wing. Note that each of the three bivalue cells in the XY-Wing is itself an ALS, hence we can set C as the pivot cell, and the other two pincer cells as A and B respectively.

Recall that the XY-Wing is a chain of length three, and can be generalized to XY-Chain, which is a chain of arbitrarily length. Similarly, we can generalize ALS-XY-Wing to ALS-XY-Chain, which is a chain whose nodes are ALSs instead of single cells.

Example

This example is taken from Ron Moore's walkthrough for Ruud's 2007 May 5 Nightmare.

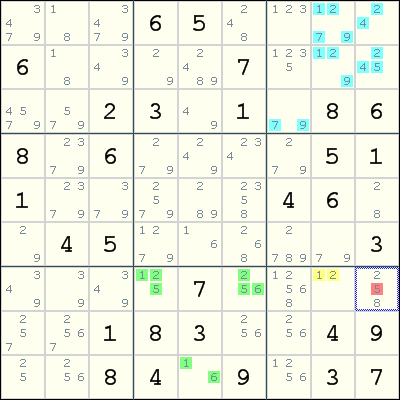
image:ALSXYWingExample.png

The ALS-XYZ-Wing is constructed as follows:

The ALS A is the cells colored green in box 8,
The ALS B is the cells colored light blue in box 3,
The ALS C is the cell colored yellow in box 9,
The restricted common Y between A and C is 2, and
The restricted common Z between B and C is 1.

The cells r7c46 in ALS A and the cell r2c9 in ALS B contain the candidate 5. Since all of r7c46 and r2c9 have a common peer r7c9, we can eliminate 5 from r7c9.

A possible Eureka notation for this elimination is:

(5=24791)ALS:r12c89,r3c8 - (1=2)r7c8 - (216=5)ALS:r7c46,r9c5 => r7c9 <> 5

Note, the reader must check the grid to ensure that r7c9 can see all the 5's in both ALS's and similarly for the links involving digits 1 and 2.

Using the ALS (245)r12c9 and a group node for (2)r12c8 we could also use ALS nodes in an AIC:

(5=42)ALS:r12c9 - (2)r12c8 = (2)r7c8 - (216=5)ALS:r7c46,r9c5 => r7c9 <> 5

which provides greater freedom for the locations of candidates in box 3.

In this example, since the pivot ALS C is a single cell, we can replicate the same elimination using Death Blossom instead.

2-Box ALS-XT-Wing Example

The previous example is excellent but it is one of the most difficult ALS-XY-Wing examples to spot. The 2-Box example shown below is one of the easiest and perhaps most frequently occuring ALS-XY-Wing. In this example the pivot ALS(12) is r2c2, one pincer ALS(23) is r2c6, and the other pincer ALS(138) is r1c12. Note that this closely resembles a 2-Box XY-Wing, except that the 138 ALS is used in place of a 13 cell. It also works in exactly the same manner and 3 can be eliminated from r1c9, since 3 is either in r2c6 or in the 138 ALS, depending on the pivot value. After this elimination the puzzle is easily solved using basic techniques.

One could argue that this would be an ALS-XZ example if r2c2 and r2c6 are grouped together, but this is irrevalent since the same statement could be made for any XY-Wing.

2-Box ALS-XY-Wing Example[code]

|-----------------+-----------------+------------------|
|  38   18    6   | 134    2    9   |   5    7   1-34  |
| 235   12    9   |   8  145    7   |  23  124     6   |
| 2357   4  1257  | 135   15    6   |   9   12     8   |
|-----------------+-----------------+------------------|
| 245    6   25   |   9    7   235  |  38  148   134   |
|   1    9  278   | 2346 468   238  |  67    5    34   |
| 4578   3  578   | 1456 14568 158  |  67    9     2   |
|-----------------+-----------------+------------------|
|  28    5    3   |   7  168   128  |   4  268     9   |
|   6  1278 1278  |  25    9    4   |  28    3    57   |
|   9   278   4   | 256    3   258  |   1  268    57   |
|-----------------+-----------------+-----------------| [/code]

The original puzzle is:

006020570 009800006 040006008 000970000 100000050 030000002 053700400 600004030 900030100

Notes on notation

Unlike ALS-XZ and XY-Wing, which eliminates the digit Z, the ALS-XY-Wing eliminates the digit X instead. Unfortunately, this inconsistent notation is widely used by the Sudoku community.

External link

Almost locked rules (for now)