---

45 rule

The 45 rule is a basic solving-technique in Killer Sudoku. Each house (row, column, nonet) must add to 45 (the sum of the digits 1 through 9). If a set of cages fits nearly exactly into one or more houses, then the contents of the leftover cells may be deduced from the difference between the sum of the cages and 45 times the number of houses.

For instance, consider this puzzle:

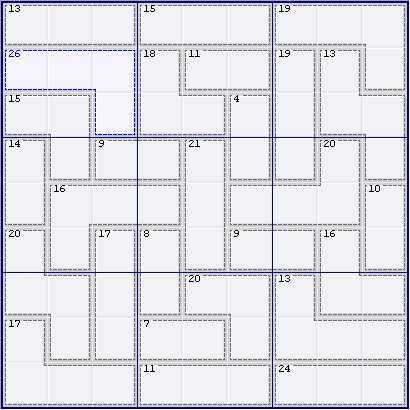
We can use the 45 rule on N9 (nonet 9) by adding together the three cages in N9 and subtracting 45:

24 + 16 + 13 - 45 = 8

Therefore R6C8 = 8. In cases like this, where there are one or more "extra" cells, the extra cells are known as outies.

Sometimes the converse occurs: one or more cells are "missing" (logically enough, they are called innies). In the above puzzle, we can use the 45 rule on N8 to deduce the value of the innie cell R7C4. In this case we must subtract the cage sums from 45:

45 - (20 + 7 + 11) = 7

We can use the 45 rule on any house, not just nonets; for instance, in this puzzle, we can deduce the value of R2C9 as 13 + 15 + 19 - 45 = 2.

We can also use the 45 rule on multiple (but non-overlapping!) houses. (In the case of overlaps, a different set of rules comes into play.) For instance, in the puzzle above, we can deduce the sum of R45C4 by applying the 45 rule to nonets 1, 4 and 7 (N147), by adding together the sums of all cages within those nonets and subtracting 45 x 3 = 135:

13 + 26 + 15 + 14 + 9 + 16 + 20 + 17 + 17 - 135 = 12

Therefore R45C4 = 12. In other words, we have created a "new" two-cell cage, which is known as a split cage or hidden cage.

Sometimes it is impossible to split a cage cleanly off, but it is nonetheless possible to deduce the relation between cells via the innie-outie difference (q.v.).

This page was last modified 22:06, 19 February 2007.  

---