---

Weak Link Square

Weak link squares are a property of several sudoku variants. A weak link square is a set of four cells that are not all in one group (line, diagonal ...) and of that each pair of cells is weak linked. So its impossible that any two cells of this square have the same value.

The following diagrams shows 3 types of weak link squares in Sudoku-X:

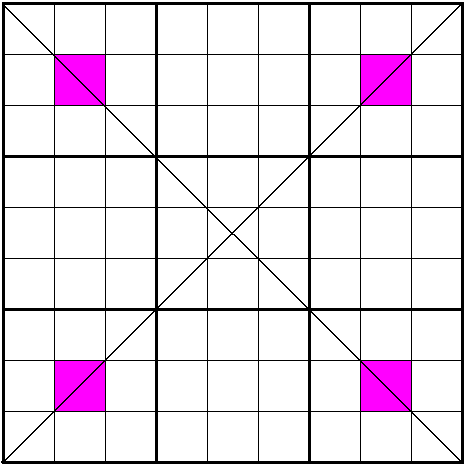
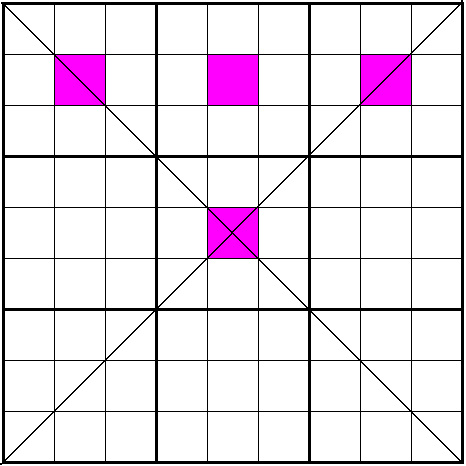
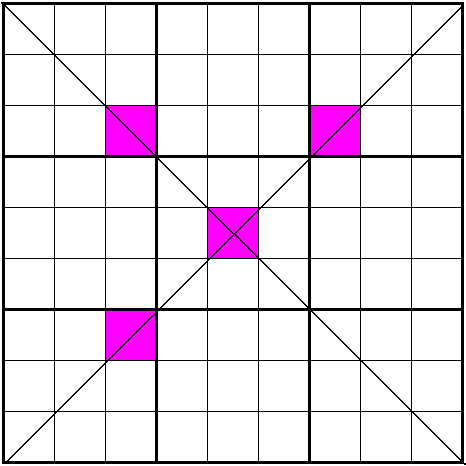
In weak link squares there work techniques like naked pairs and naked triples.

If we have additional that in such a square there are only 4 different candidates at all then also many other techniques like hidden single/hidden pair/hidden triple, weak link square-line interaction, weak link square-diagonal interaction, pointing pair, pointing triple and pointing quad work.

Adding as 5th cell R5C5 to weak link squares of the first type we get weak link pentagons with similar properties. There exist in many sudoku variants also weak link triangles.

There are also Skewed Fishs where the defining sets are diagonals and the secondary sets are weak link squares. Here a Mutant X-Wing of this type:

The X-Wing with candidate 1 is formed by the pink cells because the yellow cells doesn't contain this candidate.. The defining set are the diagonals and the secondary set the weak link squares R258C2+R5C5 and R357C7+R5C5. We can conclude for the green cells that they can't have candidate 1.

This page was last modified 18:21, 13 January 2008.  

---