---

W-Wing

A W-Wing is formed by a chain of four cells:

• A: A cell with two candidates W and X.
• B: A cell with X as a candidate.
• C: A cell with X as a candidate.
• D: A cell with two candidates W and X.

It is required that A sees B, C sees D, and B and C has a strong link on the digit X. Then W can be eliminated from any cell that is seen by both A and D.

Suppose T is a cell that is seen by both A and D, and T contains W as a candidate. Then, the W-Wing can be written as follows in Nice Loop notation:

[T]-W-[A]-X-[B]=X=[C]-X-[D]-W-[T] => T<>W

Example

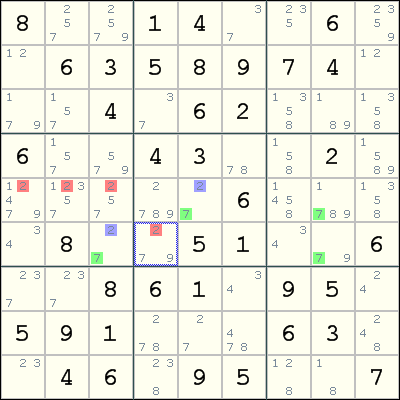
In this grid, note the r5c5 and r6c3 cells with the candidates 2 and 7. Also, the green 7 candidates form a chain, with r5c8 and r6c8 forming a strong link (because r5c8 and r6c8 are the only cells with candidate 7 in this box). Hence, we can eliminate the digit 2 from all cells that are seen by both r5c5 and r6c3, i. e., those marked in red.

Doubly Linked W-Wing Example

In a doubly-linked W-Wing the identical pairs are linked to 2 digit conjugate pairs rather than a single digit conjugate pair as in the previous example. This is illustrated in the following example where the 17 cells r8c4 and r9c8 are linked to the 7 conjugate pair and the 1 grouped conjugate in box 7. This means that both 1 and 7 must occur either in r8c4 or r9c8. Each of these are conjugate with the 17 conjugates in box 7. Therefore 1 and 7 can be eliminated from other cells in rows 8 or 9. Candidate eliminations are indicated with a -.

Doubly Linked W-Wing Example

|-----------------+-----------------+-----------------|
|   5   67    3   |   9    2   68   |   4   178  16   |
|   4   167  168  |   5   67    3   |  678   9    2   |
|  89    2   689  |  17    4   168  |  678   5    3   |
|-----------------+-----------------+-----------------|
|   3    4    7   |   2   19   19   |   5    6    8   |
|   6    9    2   |   8    5    7   |   1    3    4   |
|   1    8    5   |   6    3    4   |   9    2    7   |
|-----------------+-----------------+-----------------|
|   2    5    4   |   3  1679  169  |  678  178  169  |
|  789  16  1689  |  17 -16-79  2   |   3    4    5   |
|  79    3   169  |   4    8    5   |   2   17  -169  |
|-----------------+-----------------+-----------------|

External Link

• The W-Wing

This page was last modified 17:54, 23 April 2009.  

---