Mirrored from Sudopedia, the Free Sudoku Reference Guide

Law of Leftovers

The Law of Leftovers is a solving technique that operates on Sudoku Variations with irregular regions, such as Jigsaw Sudoku. The technique was devised by Bob Harris.

The technique is based on the fact that an equal number of houses must have an equal number of occurrences for each digit.

Selecting Law of Leftovers regions

It may be difficult at first to find the best spots to apply this technique, but there is a method to quickly identify the most promising areas in the grid. Just look for borders between rows or columns which largely coincide with jigsaw borders. In the example, the border between column 6 and 7 has 5 cell borders which are also the border of jigsaw regions.

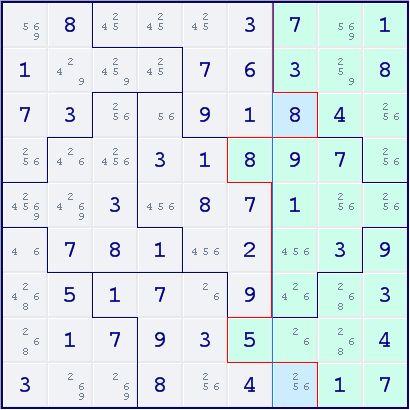
Draw a line separating a certain number of jigsaw regions.

In the example, the red line separates the 3 light green jigsaw regions.

Draw a line separating the same number of rows or columns.

In the example, the blue line separates the left 3 columns.

Identify the parts of the jigsaw regions outside the separated rows or columns.

The example below has 2 cells sticking out.

Identify the parts of the remaining regions inside the separated rows or columns.

In the example, these parts have a light blue color.

Verify that the number of innies and outies are the same.

There are 2 green outies and 2 blue innies in the example.

Compare the innies and the outies.

See the next section for Law of Leftovers logic.

Comparing the innies and the outies

In the example, we see that one of the outies (r4c6) contains digit 8. The green cells inside the last 3 columns only have room for 2 more instances of digit 8. The innies must therefore supply the missing digit 8. Fortunately, r3c7 already contains digit 8, so this condition is satisfied.

The other outie contains digit 5. Again, the blue innies must compensate this loss. There is only one innie left, so we can place digit 5 in r9c7.

The Law of Leftovers states that in the solution, the innies and the outies contain the same digits. From this law, we can make the following deductions:

A digit placed in an outie must also be placed in one of the innies.
A digit placed in an innie must also be placed in one of the outies.
A digit for which no outie has any candidates can be eliminated from all innies.
A digit for which no innie has any candidates can be eliminated from all outies.
When all innies belong to the same line, a digit which must be placed in one of the innies can be eliminated from the other cells on that line.
When all outies belong to the same line, a digit which must be placed in one of the outies can be eliminated from the other cells on that line.

External links

This page was last modified 16:52, 10 August 2010.