---

Killer Subset

A Killer Subset is a variation of Naked Subsets and Hidden Subsets that can sometimes be found in Killer puzzles. The simplest Killer Subsets are found in many puzzles, and identifying them is a basic technique; the most complex Killer Subsets (containing 4 or 5 numbers) are comparatively rare, and are more typically found in the most difficult puzzles.

Killer Subsets are formed when a set of X digits can be shown to have exactly X candidates in a range of Y cells in a house (where Y is greater than X). In such a case, the candidates in the set may be eliminated from all cells outside of Y.

Typically – but not always – the subset of candidates will be a contiguous range (for instance, {789} or {56}).

In ordinary sudoku, subsets may be "naked" or "hidden"; and in fact every Naked Subset has its complementary Hidden Subset and vice versa. An identical logic applies to Killer Subsets, too, in that complementary logics can be used to make the same eliminations; however, the "naked/hidden" distinction is less accurate as a description, since often both versions of the logic are hard to spot ("hidden" among the candidates).

Names for each size

Killer Pair

Size 2

Killer Triple

Size 3

Killer Quad

Size 4

Killer Quint

Size 5

How it works

Here is a simple example:

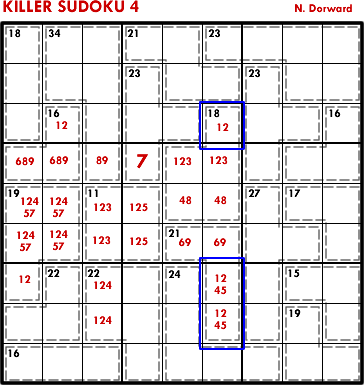
The cells R78C6 = 6 = {15} or {24}, i.e. they must contain either 1 or 2. They therefore form a naked pair in conjunction with the {12} in R3C6. This allows us to eliminate {12} for the rest of column 6, which means that R4C6 = 3.

Here is an example of a killer triple:

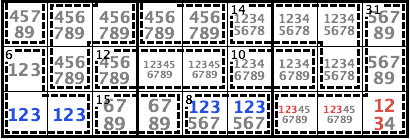
The cage 8/2 in R9C56 = {17|26|35} must include one of {123}. It forms a naked triple on {123} with the cells in R9C12 = {123}. Therefore {123} of R9 is locked in R9C1256 and can be eliminated from the rest of R9, which means R9C9 = 4.

Here is another example of a killer triple:

The cage 9/3 in R1C123 = {126|135|234} must include either {12} or {13} or {23}. It must include at least two digits out of {123}. It forms a naked triple on {123} with R1C4 = {123}. Therefore {123} of R1 is locked in R1C1234 and can be eliminated from the rest of R1.

Here is an example of a killer hidden pair:

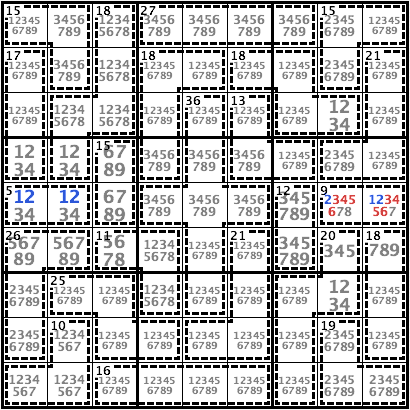
The candidates {12} of R5 are locked either in the cage 5/2 in R5C12 or in the cage 9/2 in R5C89. Neither the cage 5/2 nor the cage 9/2 may include both 1 and 2. Therefore each of these cages must include one of 1 or 2, which means the cage 9/2 in R5C89 = [81] or {27} and cannot have {36} nor {45}.

Here is a much more complex example:

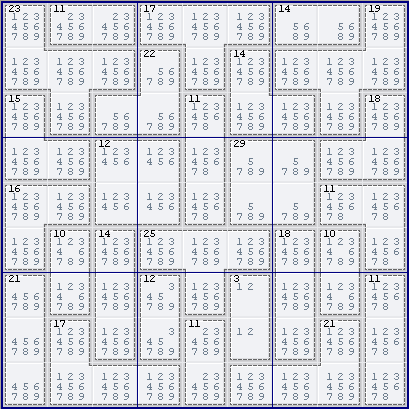
(Weekly Assassin 34 by Ruud)

In column 7, we can find a Killer Subset on {56789}. R1C7 contains {5689} and R45C7 contain {5789} – three cells out of the five we need. The other two cells are provided by the 18(3) cage at R678C7, because it must contain two cells from the subset {56789}. (This can be proved by contradiction: if it contained only one cell from {56789}, the maximum cage-sum would be 3+4+9 = 16.) Therefore we can eliminate {56789} from R239C7.

Examples of puzzles containing killer subsets of size 4 or 5

• Weekly Assassin 34 (Ruud)
• Killer 10 (ND)
• JC Godart Corresponding Killer – the first puzzle in the set contains a {1235} quad in C4.

This page was last modified 15:27, 27 May 2007.  

---