---

Gurth's Symmetrical Placement

Gurth's Symmetrical Placement is a technique for solving Sudoku puzzles with 180-degree rotational symmetry in the givens, i.e., the cell r[i]c[j] contains a given if and only if the cell r[10 - i]c[10 - j] also contains a given.

The technique is applied to a rotational symmetric puzzle as follows. Suppose for every digit n, we can find a digit k, such that for every cell in this puzzle that contains the given n, its opposite cell (i.e., the cell that is rotated about r5c5) contains the given k. Then all the other cells in this puzzle will also contain this property. Furthermore, if the r5c5 cell is empty, then r5c5 can be assigned the digit n whose opposite digit is also n, or the missing digit if the puzzle contains givens for only eight of the nine digits.

Stated another way, let the nine digits of a rotational symmetric puzzle be a1, a2, b1, b2, c1, c2, d1, d2 and e. Suppose also that for all i and j in {1, ..., 9}, whenever the cells r[i]c[j] and r[10 - i]c[10 - j] are non-empty, we have both cells containing {a1, a2}, {b1, b2}, {c1, c2}, {d1, d2} or {e, e}. Then the empty cells can be filled up so that the above property is satisfied. Also, if r5c5 is empty, then we can assign e to it.

The rationale for Gurth's Symmetrical Placement is that if we can apply a technique T to a group of cells S to assign a digit X to some particular cell A, then we can also apply the same technique T to the cells that are opposite to S and assign the digit that is the partner of X to the cell that is opposite to A. The puzzle is required to contain a unique solution for Gurth's Symmetrical Placement to be valid.

Example

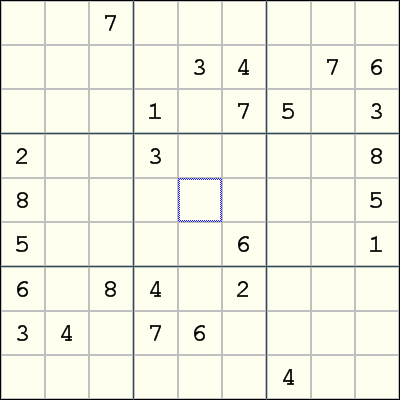
The above puzzle is difficult without using Gurth's Symmetrical Placement. However, once Gurth's Symmetrical Placement is applied, the remainder of the puzzle can be solved by singles alone. More specifically, the digit pairs are {1, 2}, {3, 6}, {4, 7}, {5, 8}, and the missing digit 9. (For example, r3c4 and r7c6 are opposites and contains 1 and 2, and r6c9 and r4c1 are also opposites and also contains {1, 2}.) So we can place 9 in r5c5, and the rest is very easy.

This page was last modified 16:38, 2 January 2008.  

---